Machine Learning Cheat Sheet

Simply excellent – includes a section of Bayesian vs Frequentist Analyses

Check out @freakonometrics’s Tweet: https://twitter.com/freakonometrics/status/602304149049495552?s=09

Survival Analysis With Generalized Additive Models: Part V (stratified baseline hazards)

In the fifth part of this series we will examine the capabilities of Poisson GAMs to stratify the baseline hazard for survival analysis. In a stratified Cox model, the baseline hazard is not the same for all individuals in the study. Rather, it is assumed that the baseline hazard may differ between members of groups, even though it will be the same for members of the same group.

Stratification is one of the ways that one may address the violation of the proportionality assumption for a categorical covariate in the Cox model. The stratified Cox model resolves the overall hazard in the study as:

In the logarithmic scale, the multiplicative model for the stratified baseline hazard becomes an additive one. In particular, the specification of a different baseline hazard for the different levels of a factor amounts to specifying an interaction between the factor and the smooth baseline hazard in the PGAM.

We turn to the PBC dataset to provide an example of a stratified analysis with either the Cox model or the PGAM. In that dataset the covariate edema is a categorical variable assuming the values of 0 (no edema), 0.5 (untreated or successfully treated) and 1(edema despite treatment). An analysis of the Schoenfeld residual test shows that this covariate violates the proportionality assumption

> f<-coxph(Surv(time,status)~trt+age+sex+factor(edema),data=pbc)
> Schoen<-cox.zph(f)
> Schoen
rho chisq p
trt -0.089207 1.12e+00 0.2892
age -0.000198 4.72e-06 0.9983
sexf -0.075377 7.24e-01 0.3950
factor(edema)0.5 -0.202522 5.39e+00 0.0203
factor(edema)1 -0.132244 1.93e+00 0.1651
GLOBAL NA 8.31e+00 0.1400
> 

To fit a stratified GAM model, we should transform the dataset to include additional variables, one for each level of the edema covariate. To make the PGAM directly comparable to the stratified Cox model, we have to fit the former without an intercept term. This requires that we include additional dummy variables for any categorical covariates that we would to adjust our model for. In this particular case, the only other additional covariate is the female gender:

pbcGAM<-transform(pbcGAM,edema0=as.numeric(edema==0),
edema05=as.numeric(edema==0.5),edema1=as.numeric(edema==1),
sexf=as.numeric(sex=="f"))

 

Then the stratifed Cox and PGAM models are fit as:

fGAM<-gam(gam.ev~s(stop,bs="cr",by=edema0)+s(stop,bs="cr",by=edema05)+
s(stop,bs="cr",by=edema1)+trt+age+sexf+offset(log(gam.dur))-1,
data=pbcGAM,family="poisson",scale=1,method="REML")

fs<-coxph(Surv(time,status)~trt+age+sex+strata(edema),data=pbc)

In general the values of covariates of the stratified Cox and the PGAM models are similar with the exception of the trt variable. However the standard error of this variable estimated by either model is so large, that the estimates are statistically no different from zero, despite their difference in magnitude

> fs
Call:
coxph(formula = Surv(time, status) ~ trt + age + sex + strata(edema), 
 data = pbc)


 coef exp(coef) se(coef) z p
trt 0.0336 1.034 0.18724 0.18 0.86000
age 0.0322 1.033 0.00923 3.49 0.00048
sexf -0.3067 0.736 0.24314 -1.26 0.21000

Likelihood ratio test=15.8 on 3 df, p=0.00126 n= 312, number of events= 125 
 (106 observations deleted due to missingness)
> summary(fGAM)

Family: poisson 
Link function: log 

Formula:
gam.ev ~ s(stop, bs = "cr", by = edema0) + s(stop, bs = "cr", 
 by = edema05) + s(stop, bs = "cr", by = edema1) + trt + age + 
 sexf + offset(log(gam.dur)) - 1

Parametric coefficients:
 Estimate Std. Error z value Pr(>|z|) 
trt 0.002396 0.187104 0.013 0.989782 
age 0.033280 0.009170 3.629 0.000284 ***
sexf -0.297481 0.240578 -1.237 0.216262 
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Approximate significance of smooth terms:
 edf Ref.df Chi.sq p-value 
s(stop):edema0 2.001 2.003 242.0 <2e-16 ***
s(stop):edema05 2.001 2.001 166.3 <2e-16 ***
s(stop):edema1 2.000 2.001 124.4 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

R-sq.(adj) = -0.146 Deviance explained = -78.4%
REML score = 843.96 Scale est. = 1 n = 3120</pre>

Survival Analysis With Generalized Additive Models : Part IV (the survival function)

The ability of PGAMs to estimate the log-baseline hazard rate, endows them with the capability to be used as smooth alternatives to the Kaplan Meier curve. If we assume for the shake of simplicity that there are no proportional co-variates in the PGAM regression, then the quantity modeled  corresponds to the log-hazard of the  survival function. Note that the only assumptions made by the PGAM is that the a) log-hazard is a smooth function, with b) a given maximum complexity (number of degrees of freedom) and c) continuous second derivatives. A PGAM provides estimates of the log-hazard constant, , and the time-varying deviation, . These can be used to predict the value of the survival function, , by approximating the integral appearing in the definition of by numerical quadrature.

From the above definition it is obvious that the value of the survival distribution at any given time point is a non-linear function of the PGAM estimate. Consequently, the predicted survival value, , cannot be derived in closed form; as with all non-linear PGAM estimates, a simple Monte Carlo simulation algorithm may be used to derive both the expected value of and its uncertainty. For the case of the survival function, the simulation steps are provided in Appendix (Section A3) of our paper. The following R function can be used to predict the survival function and an associated confidence interval at a grid of points. It accepts as arguments a) the vector of time points, b) a PGAM object for the fitted log-hazard function, c) a list with the nodes and weights of a Gauss-Lobatto rule for the integration of the predicted survival, d) the number of Monte Carlo samples to obtain and optionally e) the seed of the random number generation. Of note, the order of the quadrature used to predict the survival function is not necessarily the same as the order used to fit the log-hazard function.

## Calculate survival and confidence interval over a grid of points
## using a GAM
SurvGAM<-Vectorize(function(t,gm,gl.rule,CI=0.95,Nsim=1000,seed=0)
##         t : time at which to calculate relative risk
##        gm : gam model for the fit
##   gl.rule : GL rule (list of weights and nodes)
##        CI : CI to apply
##      Nsim : Number of replicates to draw
##      seed : RNG seed
{
q<-(1-CI)/2.0
## create the nonlinear contrast
pdfnc<-data.frame(stop=t,gam.dur=1)
L<-length(gl.rule$x)
start<-0; ## only for right cens data
## map the weights from [-1,1] to [start,t]
gl.rule$w<-gl.rule$w*0.5*(t-start)
## expand the dataset
df<-Survdataset(gl.rule,pdfnc,fu=1)
## linear predictor at each node
Xp <- predict(gm,newdata=df,type="lpmatrix")
## draw samples
set.seed(seed)
br <- rmvn(Nsim,coef(gm),gm$Vp)
res1<-rep(0,Nsim)
for(i in 1:Nsim){
## hazard function at the nodes
hz<-exp(Xp%*%br[i,])
## cumumative hazard
chz1<-gl.rule$w %*% hz[1:L,]
##survival
res1[i]<-exp(-chz1)
}
ret<-data.frame(t=t,S=mean(res1),
LCI=quantile(res1,prob=q),
UCI=quantile(res1,prob=1-q))
ret

},vectorize.args=c("t"))

The function makes use of another function, Survdataset, that expands internally the vector of time points into a survival dataset. This dataset is used to obtain predictions of the log-hazard function by calling the predict function from the mgcv package.

## Function that expands a prediction dataset
## so that a GL rule may be applied
## Used in num integration when generating measures of effect
Survdataset<-function(GL,data,fu)
## GL  : Gauss Lobatto rule
## data: survival data
##   fu: column number containing fu info

{
## append artificial ID in the set
data$id<-1:nrow(data)
Gllx<-data.frame(stop=rep(GL$x,length(data$id)),
t=rep(data[,fu],each=length(GL$x)),
id=rep(data$id,each=length(GL$x)),
start=0)
## Change the final indicator to what
## was observed, map node positions,
## weights from [-1,1] back to the
## study time
Gllx<-transform(Gllx,
stop=0.5*(stop*(t-start)+(t+start)))
## now merge the remaining covariate info

Gllx<-merge(Gllx,data[,-c(fu)])
nm<-match(c("t","start","id"),colnames(Gllx))
Gllx[,-nm]
}

The ability to draw samples from the multivariate normal distribution corresponding to the model estimates and its covariance matrix is provided by another function, rmvn:

## function that draws multivariate normal random variates with
## a given mean vector and covariance matrix
##    n : number of samples to draw
##   mu : mean vector
##  sig : covariance matrix
rmvn <- function(n,mu,sig) { ## MVN random deviates
L <- mroot(sig);m <- ncol(L);
t(mu + L%*%matrix(rnorm(m*n),m,n))
}

To illustrate the use of these functions we revisit the PBC example from the 2nd part of this blog series. Firstly, let’s obtain a few Gauss-Lobatto lists of weights/nodes for the integration of the survival function:

## Obtain a few Gauss Lobatto rules to integrate the survival
## distribution
GL5<-GaussLobatto(5);
GL10<-GaussLobatto(10);
GL20<-GaussLobatto(20);

Subsequently, we fit the log-hazard rate to the coarsely (5 nodes) and more finely discretized (using a 10 point Gauss Lobatto rule) versions of the PBC dataset, created in Part 2. The third command obtains the Kaplan Meier estimate in the PBC dataset.

fSurv1<-gam(gam.ev~s(stop,bs="cr")+offset(log(gam.dur)),
data=pbcGAM,family="poisson",scale=1,method="REML")
fSurv2<-gam(gam.ev~s(stop,bs="cr")+offset(log(gam.dur)),
data=pbcGAM2,family="poisson",scale=1,method="REML")

KMSurv<-survfit(Surv(time,status)~1,data=pbc)

We obtained survival probability estimates for the 6 combinations of time discretization for fitting (either a 5 or 10th order Lobatto rule) and prediction (a 5th, 10th or 20th order rule):

t<-seq(0,4500,100)
s1<-SurvGAM(t,fSurv1,GL5)
s2<-SurvGAM(t,fSurv1,GL10)
s3<-SurvGAM(t,fSurv1,GL20)
s4<-SurvGAM(t,fSurv2,GL5)
s5<-SurvGAM(t,fSurv2,GL10)
s6<-SurvGAM(t,fSurv2,GL20)

In all cases 1000 Monte Carlo samples were obtained for the calculation of survival probability estimates and their pointwise 95% confidence intervals. We can plot these against the Kaplan Meier curve estimates:

par(mfrow=c(2,3))
plot(KMSurv,xlab="Time (days)",ylab="Surv Prob",ylim=c(0.25,1),main="Fit(GL5)/Predict(GL5)")
lines(s1[1,],s1[2,],col="blue",lwd=2)
lines(s1[1,],s1[3,],col="blue",lwd=2,lty=2)
lines(s1[1,],s1[4,],col="blue",lwd=2,lty=2)

plot(KMSurv,xlab="Time (days)",ylab="Surv Prob",ylim=c(0.25,1),main="Fit(GL5)/Predict(GL10)")
lines(s2[1,],s2[2,],col="blue",lwd=2)
lines(s2[1,],s2[3,],col="blue",lwd=2,lty=2)
lines(s2[1,],s2[4,],col="blue",lwd=2,lty=2)

plot(KMSurv,xlab="Time (days)",ylab="Surv Prob",ylim=c(0.25,1),main="Fit(GL5)/Predict(GL20)")
lines(s3[1,],s3[2,],col="blue",lwd=2)
lines(s3[1,],s3[3,],col="blue",lwd=2,lty=2)
lines(s3[1,],s3[4,],col="blue",lwd=2,lty=2)

plot(KMSurv,xlab="Time (days)",ylab="Surv Prob",ylim=c(0.25,1),main="Fit(GL10)/Predict(GL5)")
lines(s4[1,],s4[2,],col="blue",lwd=2)
lines(s4[1,],s4[3,],col="blue",lwd=2,lty=2)
lines(s4[1,],s4[4,],col="blue",lwd=2,lty=2)

plot(KMSurv,xlab="Time (days)",ylab="Surv Prob",ylim=c(0.25,1),main="Fit(GL10)/Predict(GL10)")
lines(s5[1,],s5[2,],col="blue",lwd=2)
lines(s5[1,],s5[3,],col="blue",lwd=2,lty=2)
lines(s5[1,],s5[4,],col="blue",lwd=2,lty=2)

plot(KMSurv,xlab="Time (days)",ylab="Surv Prob",ylim=c(0.25,1),main="Fit(GL10)/Predict(GL20)")
lines(s6[1,],s6[2,],col="blue",lwd=2)
lines(s6[1,],s6[3,],col="blue",lwd=2,lty=2)
lines(s6[1,],s6[4,],col="blue",lwd=2,lty=2)

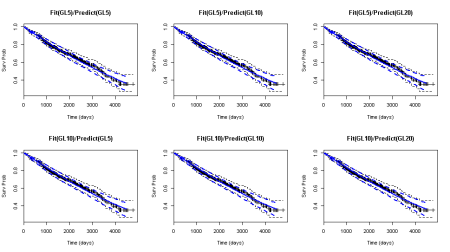
Survival probability estimates: Kaplan Meier curve (black) v.s. the PGAM estimates for different orders of Gauss Lobatto (GL) quadrature

Overall, there is a close agreement between the Kaplan Meier estimate and the PGAM estimates despite the different function spaces that the corresponding estimators “live”: the space of all piecewise constant functions (KM) v.s. that of the smooth functions with bounded, continuous second derivatives (PGAM). Furthermore, the 95% confidence interval of each estimator (dashed lines) contain the expected value of the other estimator. This suggests that there is no systematic difference between the KM and the PGAM survival estimators. This was confirmed in simulated datasets (see Fig 2 in our PLoS One paper).

Survival Analysis With Generalized Additive Models : Part III (the baseline hazard)

In the third part of the series on survival analysis with GAMs we will review the use of the baseline hazard estimates provided by this regression model. In contrast to the Cox mode, the log-baseline hazard is estimated along with other quantities (e.g. the log hazard ratios) by the Poisson GAM (PGAM) as:

In the aforementioned expression, the baseline hazard is equivalently modeled as a time-varying deviation () from a constant (the intercept ) , or as a time-varying function (). In the latter case, the constant is absorbed into the smooth term. The choice between these equivalent forms is dictated by the application at hand; in particular, the intercept may be switched on or off by centering the smooth terms appearing in the call to the gam function. Hence, in the PGAM formulation the log-baseline hazard is yet another covariate that one estimates by a smooth function; other covariates may modify this hazard in a proportional fashion by additively shifting the log-baseline hazard ().

In the “standard” way of fitting a PGAM by mgcv, the log-baseline hazard is estimated in the constant+deviation form. Exponentiation may be used to derive the baseline hazard and its standard errors. Continuing the analysis of the Primary Biliary Cirrhosis example from the second part of the series, we may write:

par(mfrow=c(2,2))
plot(fGAM,main="Gauss Lobatto (5)",ylab="log-basehaz")
plot(fGAM2,main="Gauss Lobatto (10)",ylab="log-basehaz")
plot(fGAM,main="Gauss Lobatto (5)",ylab="basehaz",trans=exp)
plot(fGAM2,main="Gauss Lobatto (10)",ylab="basehaz",trans=exp)

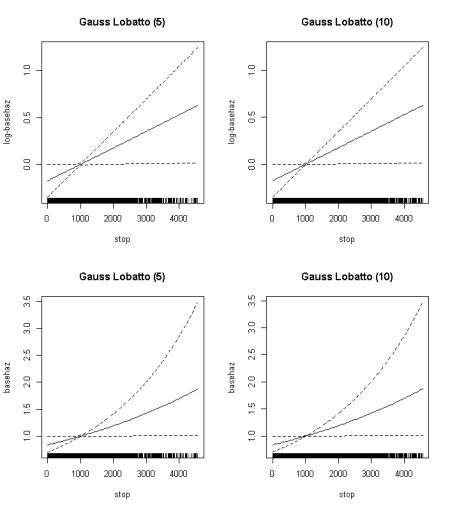
Log Baseline (top row) and Baseline (second row) hazard function in the PBC dataset for two different discretizations of the data. In all these cases, the baseline hazard (or its log) are given as time varying deviations from a constant (the value of the log-hazard where the confidence interval vanishes)

There is no substantial difference in the estimated obtained by the coarse (Gauss Lobatto (5)) and finer (Gauss Lobatto (10)) discretization. Note that as a result of fitting the log-hazard as constant+ time-varying deviation, the standard error of the curve vanishes at ~1050: the value of the log-hazard at that instant in events per unit time is provided by the intercept term.

Estimation of the log-baseline hazard allows the PGAM to function as a parametric, smooth alternative to the Kaplan Meier estimator. This will be examined in the fourth part of this series.

 

Survival Analysis With Generalized Models: Part II (time discretization, hazard rate integration and calculation of hazard ratios)

In the second part of the series we will consider the time discretization that makes the Poisson GAM approach to survival analysis possible.

Consider a set of s individual observations at times , with censoring indicators assuming the value of 0 if the corresponding observation was censored and 1 otherwise. Under the assumption of non-informative censoring, the likelihood of the sample is given by:

where is the hazard function. By using an interpolatory quadrature rule, one may substitute the integral with a weighted sum evaluated at a distinct number of nodes.

where ,  are the nodes, weights of the integration rule and is an indicator variable equal to 1 if the corresponding node corresponds to an event time and zero otherwise.  By including additional “pseudo-observations” at the nodes of the quadrature rule, we converted the survival likelihood to the kernel of a Poisson regression with variable exposures (weights).  Conditional on the adoption of an efficient quadrature rule, this is a highly accurate approximation:

Bounds of the Gauss Lobatto (GL) approximation error for the integration of survival data (MST=Mean Survival Time).

In order for the construct to work one has to ensure that the corresponding lifetimes are mapped to a node of the integration scheme.  In our paper, this was accomplished by the adoption of the Gauss-Lobatto rule. The nodes and weights of the Gauss-Lobatto rule (which is defined in the interval depend on the Legendre polynomials in a complex way. The following R function will calculate the weights and nodes for the N-th order Gauss Lobatto rule:

GaussLobatto<-function(N)
{
 N1<-N
 N<-N-1
 x=matrix(cos(pi*(0:N)/N),ncol=1)
 x=cos(pi*(0:N)/N)
 P<-matrix(0,N1,N1)
 xold<-2
 while (max(abs(x-xold))>2.22044604925031e-16) {
 xold<-x
 P[,1]<-1 
 P[,2]<-x
 
 for (k in 2:N) {
 P[,k+1]=( (2*k-1)*x*P[,k]-(k-1)*P[,k-1] )/k;
 }
 
 x<-xold-( x*P[,N1]-P[,N] )/( N1*P[,N1] )
 
 }

 w<-2./(N*N1*P[,N1]^2);
 ret<-list(x=rev(x),w=w)
 attr(ret,"order")<-N
 ret
}

which can be called to return a list of the nodes and their weights:

> GaussLobatto(5)
$x
[1] -1.0000000 -0.6546537 0.0000000 0.6546537 1.0000000

$w
[1] 0.1000000 0.5444444 0.7111111 0.5444444 0.1000000

attr(,"order")
[1] 4

To prepare a survival dataset for GAM fitting, one needs to call this function to obtain a Gauss Lobatto rule of the required order. Once this has been obtained, the following R function will expand the (right-censored) dataset to include the pseudo-observations at the nodes of the quadrature rule:

GAMSurvdataset<-function(GL,data,fu,d)
## GL : Gauss Lobatto rule
## data: survival data
## fu: column number containing fu info
## d: column number with event indicator
 {
 ## append artificial ID in the set
 data$id<-1:nrow(data)
 Gllx<-data.frame(stop=rep(GL$x,length(data$id)),
 gam.dur=rep(GL$w,length(data$id)),
 t=rep(data[,fu],each=length(GL$x)),
 ev=rep(data[,d],each=length(GL$x)),
 id=rep(data$id,each=length(GL$x)),
 gam.ev=0,start=0)
 ## Change the final indicator to what
 ## was observed, map node positions,
 ## weights from [-1,1] back to the
 ## study time
 Gllx<-transform(Gllx,
 gam.ev=as.numeric((gam.ev | ev)*I(stop==1)),
 gam.dur=0.5*gam.dur*(t-start),
 stop=0.5*(stop*(t-start)+(t+start)))
 ## now merge the remaining covariate info
 Gllx<-merge(Gllx,data[,-c(fu,d)])
 Gllx
 }

We illustrate the use of these functions on the Primary Biliary Cirrhosis dataset that comes with R:

data(pbc)
> ## Change transplant to alive
> pbc$status[pbc$status==1]<-0
> ## Change event code of death(=2) to 1
> pbc$status[pbc$status==2]<-1
> 
> head(pbc)
 id time status trt age sex ascites hepato spiders edema bili chol albumin copper
1 1 400 1 1 58.76523 f 1 1 1 1.0 14.5 261 2.60 156
2 2 4500 0 1 56.44627 f 0 1 1 0.0 1.1 302 4.14 54
3 3 1012 1 1 70.07255 m 0 0 0 0.5 1.4 176 3.48 210
4 4 1925 1 1 54.74059 f 0 1 1 0.5 1.8 244 2.54 64
5 5 1504 0 2 38.10541 f 0 1 1 0.0 3.4 279 3.53 143
6 6 2503 1 2 66.25873 f 0 1 0 0.0 0.8 248 3.98 50
 alk.phos ast trig platelet protime stage
1 1718.0 137.95 172 190 12.2 4
2 7394.8 113.52 88 221 10.6 3
3 516.0 96.10 55 151 12.0 4
4 6121.8 60.63 92 183 10.3 4
5 671.0 113.15 72 136 10.9 3
6 944.0 93.00 63 NA 11.0 3
> 
> GL<-GaussLobatto(5)
> pbcGAM<-GAMSurvdataset(GL,pbc,2,3)
> head(pbcGAM)
 id stop gam.dur t ev gam.ev start trt age sex ascites hepato spiders
1 1 0.00000 20.0000 400 1 0 0 1 58.76523 f 1 1 1
2 1 69.06927 108.8889 400 1 0 0 1 58.76523 f 1 1 1
3 1 200.00000 142.2222 400 1 0 0 1 58.76523 f 1 1 1
4 1 330.93073 108.8889 400 1 0 0 1 58.76523 f 1 1 1
5 1 400.00000 20.0000 400 1 1 0 1 58.76523 f 1 1 1
6 2 0.00000 225.0000 4500 0 0 0 1 56.44627 f 0 1 1
 edema bili chol albumin copper alk.phos ast trig platelet protime stage
1 1 14.5 261 2.60 156 1718.0 137.95 172 190 12.2 4
2 1 14.5 261 2.60 156 1718.0 137.95 172 190 12.2 4
3 1 14.5 261 2.60 156 1718.0 137.95 172 190 12.2 4
4 1 14.5 261 2.60 156 1718.0 137.95 172 190 12.2 4
5 1 14.5 261 2.60 156 1718.0 137.95 172 190 12.2 4
6 0 1.1 302 4.14 54 7394.8 113.52 88 221 10.6 3
> 
> dim(pbc)
[1] 418 20
> dim(pbcGAM)
[1] 2090 24

The original (pbc) dataset has been expanded to include the pseudo-observations at the nodes of the Lobatto rule. There are multiple records (5 per individual in this particular case) as can be seen by examining the data for the first patient (id=1). The corresponding times are found in the variable stop, their associated weights in the variable gam.dur and the event indicators are in the column gam.ev. Note that nodes and weights are expressed on the scale of the survival dataset, not in the scale of the Lobatto rule (). To fit the survival dataset one needs to load the mgcv package and fit a Poisson GAM, using a flexible (penalized spline) for the log-hazard rate function.

The following code will obtain an adjusted (for age and sex) hazard ratio using the PGAM or the Cox model:

library(survival) ## for coxph
> library(mgcv) ## for mgcv
> 
> ## Prop Hazards Modeling with PGAM
> fGAM<-gam(gam.ev~s(stop,bs="cr")+trt+age+sex+offset(log(gam.dur)),
+ data=pbcGAM,family="poisson",scale=1,method="REML")
> 
> ## Your Cox Model here
> f<-coxph(Surv(time,status)~trt+age+sex,data=pbc)
> 
> 
> summary(fGAM)

Family: poisson 
Link function: log

Formula:
gam.ev ~ s(stop, bs = "cr") + trt + age + sex + offset(log(gam.dur))

Parametric coefficients:
 Estimate Std. Error z value Pr(>|z|) 
(Intercept) -10.345236 0.655176 -15.790 < 2e-16 ***
trt 0.069546 0.181779 0.383 0.702 
age 0.038488 0.008968 4.292 1.77e-05 ***
sexf -0.370260 0.237726 -1.558 0.119 
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:
 edf Ref.df Chi.sq p-value 
s(stop) 1.008 1.015 4.186 0.0417 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

R-sq.(adj) = -0.249 Deviance explained = 2.25%
-REML = 693.66 Scale est. = 1 n = 1560
> f
Call:
coxph(formula = Surv(time, status) ~ trt + age + sex, data = pbc)


 coef exp(coef) se(coef) z p
trt 0.0626 1.065 0.182 0.344 7.3e-01
age 0.0388 1.040 0.009 4.316 1.6e-05
sexf -0.3377 0.713 0.239 -1.414 1.6e-01

Likelihood ratio test=22.5 on 3 df, p=5.05e-05 n= 312, number of events= 125 
 (106 observations deleted due to missingness)

The estimates for log-hazard ratio of the three covariates (trt, age, and female gender) are numerically very close. Any numerical differences reflect the different assumptions made about the baseline hazard: flexible spline (PGAM) v.s. piecewise exponential (Cox).

Increasing the number of nodes of the Lobatto rule does not materially affect the estimates of the PGAM:

GL<-GaussLobatto(10)
> pbcGAM2<-GAMSurvdataset(GL,pbc,2,3)
> fGAM2<-gam(gam.ev~s(stop,bs="cr")+trt+age+sex+offset(log(gam.dur)),
+ data=pbcGAM2,family="poisson",scale=1,method="REML")
> 
> summary(fGAM2)

Family: poisson 
Link function: log

Formula:
gam.ev ~ s(stop, bs = "cr") + trt + age + sex + offset(log(gam.dur))

Parametric coefficients:
 Estimate Std. Error z value Pr(>|z|) 
(Intercept) -10.345288 0.655177 -15.790 < 2e-16 ***
trt 0.069553 0.181780 0.383 0.702 
age 0.038487 0.008968 4.292 1.77e-05 ***
sexf -0.370340 0.237723 -1.558 0.119 
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:
 edf Ref.df Chi.sq p-value 
s(stop) 1.003 1.005 4.163 0.0416 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

R-sq.(adj) = -0.124 Deviance explained = 1.7%
-REML = 881.67 Scale est. = 1 n = 3120

Nevertheless, the estimates of the “baseline log-hazard” become more accurate (decreased standard errors and significance of the smooth term) as the number of nodes increases.

In simulations (see Fig 3) we show that the estimates of the hazard ratio generated by the GAM are comparable in bias, variance and coverage to those obtained by the Cox model. Even though this is an importance benchmark for the proposed method, it does not provide a compelling reason for replacing  the Cox model with the PGAM. In fact, the advantages of the PGAM will only become apparent once we consider contexts which depend on the baseline hazard function, or problems in which the proportionality of hazards assumption is violated. So stay tuned.

Survival Analysis With Generalized Additive Models : Part I (background and rationale)

After a really long break, I’d will resume my blogging activity. It is actually a full circle for me, since one of the first posts that kick started this blog, matured enough to be published in a peer-reviewed journal last week. In the next few posts I will use the R code included to demonstrate the survival fitting capabilities of Generalized Additive Models (GAMs) in real world datasets. The first post in this series will summarize the background, rationale and expected benefits to be realized by adopting GAMs from survival analysis.

In a nutshell, the basic ideas of the GAM approach to survival analysis are the following:

1. One approximates the integral defining the survival function as a discrete sum using a quadrature rule
2. One evaluates the likelihood at the nodes of the aforementioned quadrature rule
3. A regression model is postulated for the log-hazard rate function
4. As a result of 1-3 the survival regression problem is transformed into a Poisson regression one
5. If penalized regression is used to fit the regression model, then GAM fitting software may be used for survival analysis

Ideas along the lines 1-4 have been re-surfacing in the literature ever since the Proportional Hazards Model was described. The mathematical derivations justifying Steps 1-4 are straightforward to follow and are detailed in the PLoS paper. The corresponding derivations for the Cox model are also described in a previous post.

Developments such as 1-4 were important in the first 10 years of the Cox model, since there were no off-the-shelf implementations of the partial (profile) likelihood approach. This limited the practical scope of proportional hazards modeling and set off a parallel computational line of research in how one could use other statistical software libraries to fit the Cox model.  In fact, the first known to the author application of a proportional model for the analysis of a National Institute of Health (NIH) randomized controlled trial used a software implementing a Poisson regression to calculate the hazard ratio. The trial was the NCDS trial that examined adequacy indices for the hemodialysis prescription (the description of the software was published 6 months prior to the clinical paper).  Many of these efforts were computationally demanding and died off as the Cox model was implemented in the various statistical packages after the late 80s and semi-parametric theory took off and provide a post-hoc justification for many of the nuances implicit in the Cox model.  Nevertheless, one can argue that in the era of the modern computer, no one really needs the Cox model. This technical report and the author’s work on a real world, complex dataset provides the personal background for my research on GAM approaches for survival data.

The GAM (or Poisson GAM, PGAM as called in the paper) is an extension of these old ideas (see the literature survey here and here). In particular, PGAM models the quantities that are modeled semi-parametrically (e.g. the baseline hazard) in the Cox model with parametric, flexible functions that are estimated by penalized regressio. One of the first applications of penalized regression for survival analysis is the Fine and Gray spline model, which is however not a PGAM model.  There are specific benefits to be realized from penalizing the Poisson regression and adopting GAMs  in the context of survival analysis:

• Parsimony: degrees of freedom are not wasted as penalization will seek the most parsimonious representation (fewer degrees of freedom) among the many possible functions that may fit the data
• Reduction of the analyst-degrees-of freedom: the shape of the functional relationships between survival and outcome are learned from the data. This limits the potential of someone putting a specific form for this relationship (e.g. linear v.s. quadratic) and running away with the most convenient p-value
• Multiple time scale modelling: one can model more than one time scales in a dataset (i.e. not just the study time). This is useful when adjusting for secular trends in an observational dataset or even in a randomized trial. In particular cluster randomized trials at the community level may be immune to secular trends
• Non-proportional hazards modeling: when the hazards are not proportional, the Cox model is not applicable. Many oncology datasets will demonstrate a deviation from proportionality (in fact we re-analyzed such a trial in the PLoS paper) . For a particular dataset, one would like to know whether the proportionality assumption is violated, and if so one would like to “adjust” for it. Such an adjustment will take the form of a time-varying hazard ratio function and these may be estimated with the PGAMs. In such a case, one can even extract an “average” hazard ratio while still estimating a time-varying deviation around it using the PGAM. However non-proportionality should shift the analyst to:
• Alternative measures of treatment effect: These may include relative risks, absolute risk differences of even differences in the (Restricted) Mean Survival Time. Such measures are calculated from the time varying hazard ratios using statistical simulation techniques
• Handling of correlated outcomes: Correlated outcomes may arise from center effects, multiple events in the same individual or even cluster randomization designs. The analysis of such outcomes is facilitated by the interpretation of the PGAM as a generalized linear mixed model and the introduction of the corresponding random effects and their correlation structure into the regression
• Center effects: A variety of modeling options are available including stratified hazards, fixed or random effects
• Subgroup analyses
• Time varying external covariates
• Unconditional/Conditional/Population averaged effects: The unconditional estimate is obtained by indexing the individuals with the group they are assigned to (e.g. placebo or drug in an interventional trial). The conditional estimate is obtained by introducing covariates (e.g. gender, age) into the regression to calculate effects for individuals that share these characteristics. The population effect averages over the conditional effects over all the individuals in the trial. In epidemiology it is known as the corrected group prognosis method. This was introduced in a JAMA paper almost 15 years ago as a way to generate adjusted survival probability curves
• Handling of right censored/left truncated/uncensored data

These benefits follow directly from the  mixed model equivalence between semi-parametric, penalized regression and Generalized Mixed Linear Models. An excellent, survey may be found here, while Simon Wood’s book in the GAM implementation of the mgcv package in R contains a concise presentation of these ideas.

As it stands the method presented has no software  implementation similar to the survival package in R. Even though we provide R code to run the examples in the paper, the need for the various functions may not be entirely clear. Hence the next series of posts will go over the code and the steps required to fit the PGAM using the R programming language.